- Home
- Challenger insights from the Door No. 3 team
- Understanding Statistical Significance
Understanding Statistical Significance
By Zach Cochran, VP of Media, Door No. 3
People love data. It’s true. Even if their career has nothing to do with advertising or marketing, they still love the idea of using data to inform decisions. It makes sense, right? As Gordon Gekko said to a young Bud Fox in Wall Street, “The most valuable commodity I know of is information. Wouldn’t you agree?” Why yes I would, Mr. Gekko.
But it does bring up another question. How much do we trust the information? How accurate is the data? To marketers, especially those that work primarily in the digital space, trusting our data to accurately inform our decisions is commonplace — and crucial. We spend hours every day, shoulders hunched over a screen, pouring over analytics and decoding the numbers that will make the difference between a campaign being a huge success, or a total dud. We put a lot of faith in the math, so it needs to be right every time.
So how can you be confident that the numbers you are using to determine your path forward are accurate? That’s where statistical significance comes in. In this article we’ll explain what it is and how to calculate it, using a real-world example to show you how it works.
But first, I should really warn you. We are going to do some serious nerding-out here. You know, p-values, confidence intervals and more. If that doesn’t sound like too much fun you can always check out some of our other Challenger Brand Insight Articles right here. Otherwise, class is officially in session.
The definition of statistical significance reads: “A number that expresses the probability that the result of a given experiment or study could have occurred purely by chance, indicated by margin of error or confidence level that the conclusions can be substantiated.” In other words, it tells us is if the results from a digital marketing campaign — good or bad — were real, or just the result of dumb luck or some kind of error. Pretty easy to see why statistical significance is important in digital marketing.
When Challenger Brand ShippingEasy needed to increase overall brand awareness around the holidays, we started by conducting a brand-lift study to measure the effectiveness of the campaign against that KPI. In order to determine if the results were accurate, we needed to ensure the statistical significance of the test. If you work in the space, this is something that comes up daily. Of all places, I’ve found that statistical significance is probably one of the most common topics of dialog between the media/analytics department and the creative folks. The conversation usually goes something like this:
Creative team: “Hey, that campaign went live on Monday, which ads are performing best?”
Media team: “Too early to say. We haven’t yet hit a threshold of statistical significance.”
Creative Team: [stares blankly and has another sip of locally produced organic flavored seltzer]
I can imagine that answer is frustrating to our creative team. They do amazing work and want to see if it’s making a difference in the real world. But to be sure that it is indeed working, we have to wait for the data set to reach a high point of statistical significance.
So now that we know what it is, let’s learn how to calculate it.
-
Define what you’d like to test. At this point you’ll want to state both a null and an alternative hypothesis. The null hypothesis is trying to prove that the change will not show significant results. The alternative hypothesis is what you are hoping to prove.
-
Determine your threshold. For any test you’ll have to determine a percentage threshold under which the hypothesis will be considered valid. This is known as your alpha. Obviously, the lower the alpha, the more strict your test. A threshold of five percent is standard in a lot of tests.
-
Run your test and record the results.
-
Run the chi-squared test. The chi-squared test compares the results from the above test to the expected results, or to the results you could have expected if there were no difference between what you were testing.
Now let’s get out of the textbook and use a real world scenario. Let’s say we want to test two different landing pages to determine if making a small change impacts conversion rate. In this example, we’ll say we changed the color of the CTA on the page.
Null Hypothesis - The current color of the CTA does not impact conversion rates
Alternative Hypothesis - New CTA color will impact conversion rates
If we want to make sure this test is relevant, there are two outputs we need to pay attention to:
-
The P-Value weighs the strength of the evidence against the null hypothesis. A p-value of <0.05 is the conventional threshold for declaring statistical significance.
-
Confidence intervals around effect size refers to the upper and lower bounds of what can happen with your experiment.
There are also two variables to ensure the result isn’t attributed to chance:
-
Sample Size is how large the sample in your experiment is. The larger the sample size, the more confidence you can have in your results. In our example, the more interactions users have with the two landing pages, the sooner you will have a data set large enough to determine if there are statistically significant results.
-
Effect Size refers to the size of the difference between the sample sets. If you see a large difference on your numbers you’ll be able to validate it with a smaller sample size. If you see a small difference between your numbers you will need a larger sample size to determine if the difference is significance or just chance.
Let’s take a look at the observed results of our two landing pages.
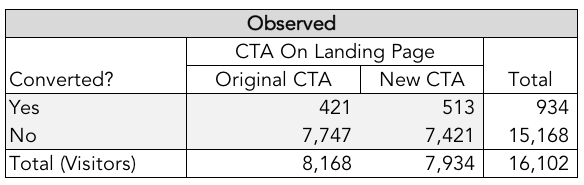
As you can see, the new landing page showed a higher conversion rate than the previous landing page. Now we need to calculate our expected results.
In the expected results the overall conversion rate will be 6% (total conversions of 934 divided by total visitors of 16,102). Now, replace the observed numbers above with the expected numbers by multiplying the column total by the row total and divide by the total visitors.
Expected Result = (column total * row total)/ total visitors
Expected = (7,934 * 934)/16,102
Expected = 460
Repeat this math for all four boxes and you’ll get the expected results chart.

Going back to the steps, this is showing us what the results would be if there were no difference between the tests. Now we’ll use the chi-squared method to compare whether the observed results are significantly different from the expected result.
To do this we will subtract the expected result from the observed result, square the result and divide that result by the expected.
Chi-Squared = (expected - observed)squared / expected
Chi-Squared = (7,474 - 7,421)squared/ 7,474
Chi-Squared = .37
Apply this math to all four boxes and you’ll have the chi-squared calculation.
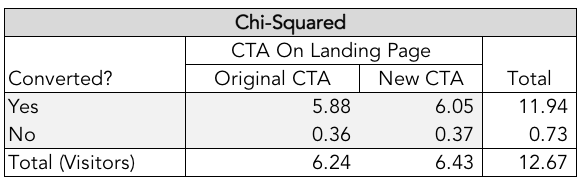
If you find that the probability (p-value) is greater than the value on the chi-squared chart for the five percent threshold then you have a test that is statistically significant. In the above example, you can see the p-value of 12.67 is greater than the five percent threshold value of 3.84 and is therefore indeed statistically significant (I did warn you that we’d be nerding out here, right?).
In the above test we see that the conversion rate between the new landing page and the old landing page is pretty close, with the new design showing an increase. However, we also now know that the results are statistically significant, and we can be confident that the change will continue to show improved results.
In conclusion, using data and testing to inform decisions is a good thing, even if the result of your test is not what you expect. But no test should be considered complete without first calculating the statistical significance of the result. From there, you can measure and test pretty much anything you can think of: A/B tests of creative, landing page conversions, subject lines for email campaigns, messaging - anything! And you can do it all with confidence because you know the results are accurate, and you can prove it.
ABOUT DOOR NO. 3
Door No. 3 is an advisor to challenger brands. Based in Austin, Texas, the award-winning advertising agency represents a diverse stable of growth clients including Cirrus Logic, Maine Root, ShippingEasy, Drunken Sailor Spirits, NIC USA, NorthStar Financial, FirstCare Health Plans, Alen Air, Cintra US and Centennial Bank. Services include brand development, creative and media planning/buying. Door No. 3's work has been recognized by publications such as The New York Times, Communication Arts, AdWeek, INC., Entrepreneur and The Wall Street Journal.
